凯利公式是由贝尔实验室的凯利提出来的一个著名的公式. 公式解决了这样的一个问题, 在一个已经胜率和赔率的游戏中, 如何确定投入的比例(仓位), 使得在长期的游戏中, 获得一个最高的预期收益.

具体来说, 如果一个游戏的胜率是p, 输的概率用q=1-p来表示, 赔率是b, 也就是说, 如果投入1, 获胜将会获得1+b(净赚b), 那么, 每次投入的仓位应为

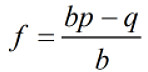
凯利公式其实不是一个公式, 更重要的是思路. 根据凯利公式的思路, 我们可以解决这样一个问题(by  @周方圆  ):

下注某可转债
1%几率亏100%
49%几率亏10%
50%几率赢20%
利用凯利公式, 求最优下注比例.

假设初始资金为X₀, 总共进行了N次下注, 每次的下注比例为f, 下注n次后资金变为Xₙ. 如果N足够大的话, 频率就会将近概率, 我们可以假设亏100%的次数为0.01N, 亏10%的次数为0.49N, 赢20%的次数为0.5N. 

由于下注的比例是f, 所以如果第n次是亏100%的话, 那么Xₙ=Xₙ₋₁(1-f); 
如果第n次是亏10%的话, 那么Xₙ=Xₙ₋₁(1-0.1f); 
如果第n次是赚20%的话, 那么Xₙ=Xₙ₋₁(1+0.2f); 

于是, 下注N次后, 资金乘了0.01N次(1-f), 0.49N次(1-0.1f), 0.5N次(1+0.2f), 即

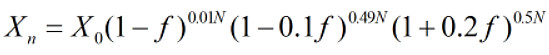
平均每次的收益率为

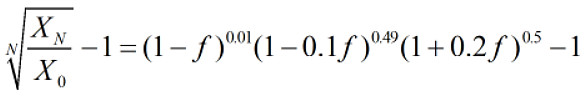
问题变成求上式右边的最大值. 而这个是关于f的一元函数, 可以借助导数的工具来求最大值.

令

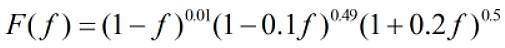
取对数得

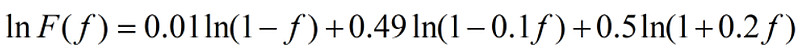
求一阶导数, 二阶导数得

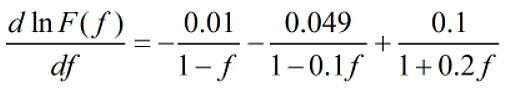
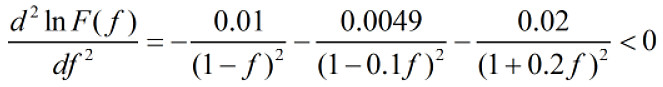
所以一阶导数为0时, F(f)取得最大值. 由

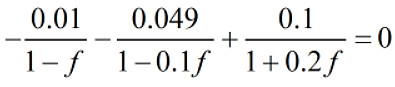
解得f约为71.24%. 这个方程可以化成二次方程, 其精确解为一正一负两根:

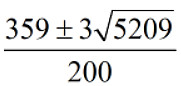
不过我偷了一下懒, 直接用计算工具得出了结果.

若每次都下注71.24%, 可以计算出平均每次收益率为1.8%.

将收益率与下注比例f的关系画成图像, 是这样子的:

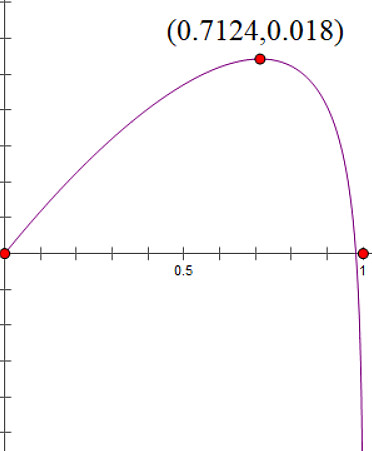
从这个图可以看到, 如果下注比例达到98%, 开始出现负的预期收益; 而如果每次都梭哈, 预期收益率将会到达惊人的-100%.

以上是凯利公式的一个简单应用. 凯利公式还可以处理更复杂的情形, 当然也需要更高级的数学工具.