风险容忍度与资产配置

前面已经说明如何建立资本配置线，即资产配置决策下所有可行的风险报酬组合构成的图形。投资者必须从可行集中选择最优的组合。这个决策包含了风险和收益的权衡选择。个人投资者风险厌恶程度不同，意味着给定相同的可行集（无风险利率和报酬-波动性比率相同），不同的投资者将选择不同的头寸。特别地，越是风险厌恶的投资者会选择更少的风险资产，更多地选择无风险资产。

一个面临无风险利率r f 和期望收益为E（r P ）、标准差为σ P 的风险资产投资者会发现，对于任意y，组合的期望收益由式（6-3）给出

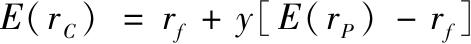
由式（6-4），整个组合的方差为

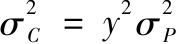
投资者试图通过选择风险资产的最优配置y使效用最大化。效用函数由式（6-1）给出，即U=E（r）-1/2Aσ 2。 当风险资产配置增加（y增加），期望收益增加，但是收益波动性也增加，因此效用可能增加也可能减少。表6-4展示了效用水平随y值变化的数据。一开始，效用随y增加而增加，最终随y增加而降低。

表6-4 风险厌恶系数A=4的投资者不同风险资产比例y带来的效用值

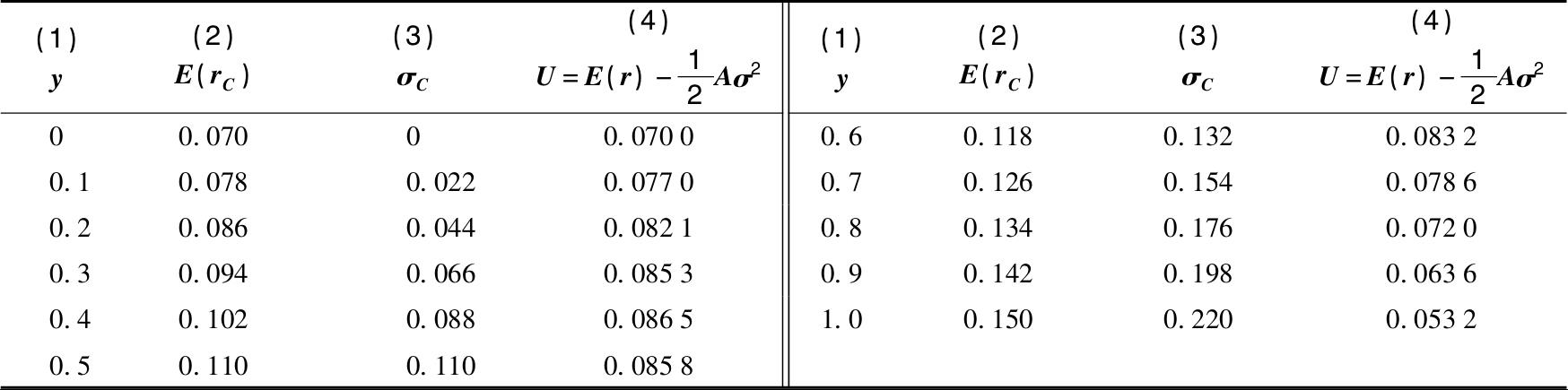
图6-6给出了表6-4中效用函数的散点图。效用在y=0.41时是最高的；当y＜0.41时，投资者愿意为更高的期望收益而增加投资风险；而当y>0.41时，风险增加效用则会降低。

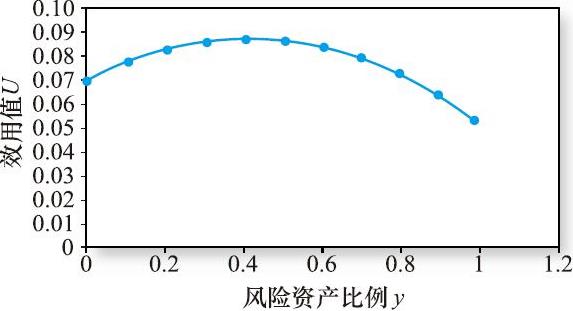
图6-6 效用值U关于风险资产比例y的函数

为了解决这一效用最大化的问题，我们把问题写作：

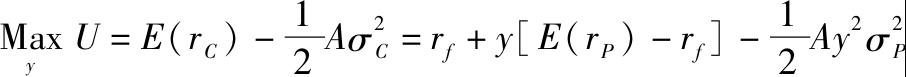
学过微积分的学生知道最大化问题是使一阶导数为零。这样求解出风险厌恶者风险资产的最优头寸y*如下

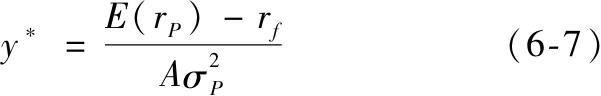
这个解显示风险资产的最优头寸正如你所预料的那样，与风险厌恶程度和风险水平（由方差表示）有关。

使用前述数字例子的数据（r f =7%，E（r P ）=15%，σ P =22%），所有收益用小数表示，一个风险厌恶系数为A=4的投资者的最优解为

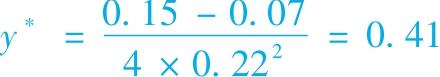
（注：对y的一阶导数等于  ，使该式为0，得到式（6-7）。）

换句话说，该投资者将会把投资预算的41%投资于风险资产，59%投资于无风险资产，如图6-6所示，此时效用达到最高水平。

当41%投资于风险资产，整个组合的期望收益和标准差为

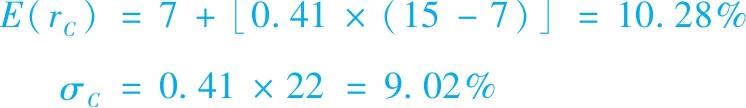
整个组合的风险溢价是E（r C ）-r f =3.28%，标准差为9.2%，注意到3.28/9.02=0.36，这正是例子中所假设的报酬-波动性比率。

这个决策的图解法是利用无差异曲线进行分析。为了理解如何构造无差异曲线，考虑风险厌恶系数A=4的一个投资者，他目前全部投资于无风险组合，收益率r f =5%。因为这个组合的方差为零，式（6-1）告诉我们它的效用为U=0.05。当投资者投资于σ=1%的风险组合时，为了获得相同的效用，其期望收益必须上升，以弥补更高的σ值：

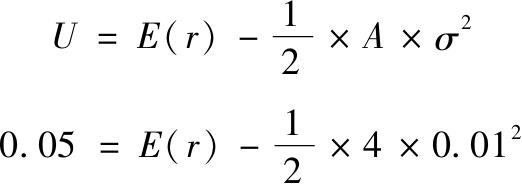
这说明必要的期望收益为

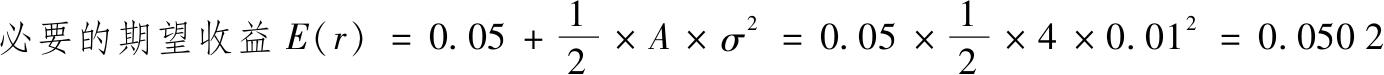
对不同的σ重复这样的计算，可以得到保证效用值为0.05所需的E（r）。这个过程将得到效用水平为0.05时所有期望收益和风险的组合。把这些组合描点在图上便得到无差异曲线。

可以使用Excel表格来生成投资者的无差异曲线。表6-5包含了效用值分别为0.05和0.09对于风险厌恶分别为A=2和A=4的两个投资者的风险和收益组合。图6-7描绘了A=2对应的期望收益和标准差组合，截距分别为0.05和0.09，对应曲线的效用水平。

表6-5 无差异曲线的数字计算

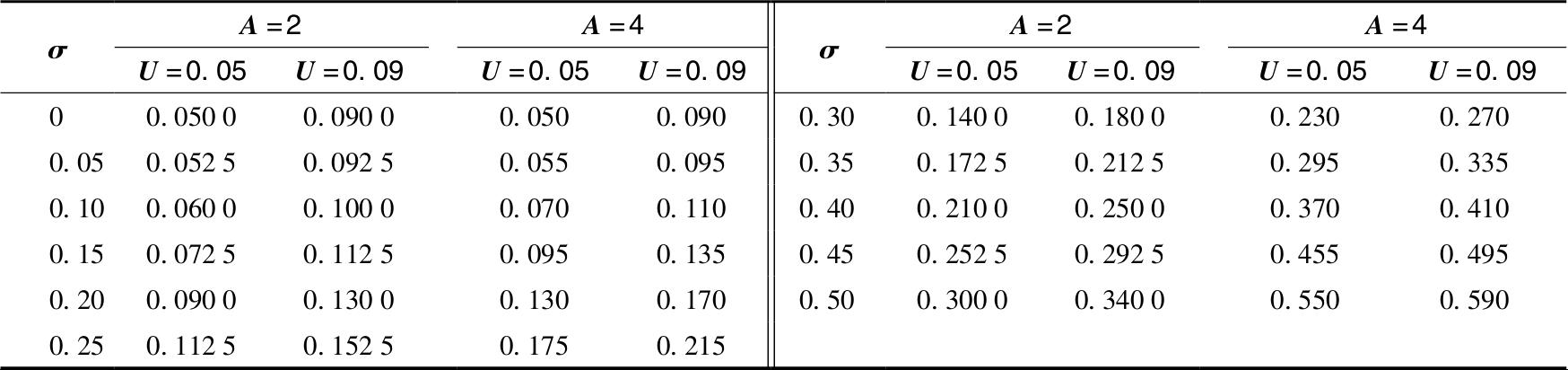
注：表中为需要达到相应效用值的期望收益。

假定任何投资者都愿意投资于更高无差异曲线上的组合，获得更高的效用。更高无差异曲线上的资本组合在给定风险水平上能够提供更高的期望收益。例如，A=2的两条无差异曲线形状相同，但是对于任意水平的风险，效用为0.09%那条曲线比0.05的那条曲线的期望收益高4%。

表6-5中的第4列和第5列对风险厌恶系数更高（A=4）的投资者重复了上述分析。图6-7反映出更高风险厌恶程度投资者的无差异曲线比低厌恶程度投资者的曲线更陡峭。更陡峭的曲线意味着投资者需要更多的期望收益来补偿同样的组合风险。

更高的无差异曲线意味着对应更高的效用水平，因此投资者更愿意在更高的无差异曲线上寻找投资组合。如图6-8所示，在表示可行集的资本配置线上加入无差异曲线，我们就可以得到与资本配置线相切的最高的无差异曲线，切点对应最优投资组合的标准差和期望收益。

关注【叩富问财】服务号，关注后在对话框回复“期货风险度”，可获得关于期货风险度的最新热点、必学知识、视频讲解、一对一顾问讲解等服务。点击微信，一键关注