长期投资

考虑一名投资者为其25年后的退休于今天储蓄了1美元，把这1美元投资于一个风险股票投资组合（获得的股利也进行再投资），这个股票组合的月收益率为1%，那么退休后他的这笔退休“基金”会增长近20倍，其终值为（1+0.01） 300 =19.79（美元）（增长了1879%）。同时比较投资于一个25年无风险月平均收益率为0.5%的国债时，投资的终值只有1.005 300 =4.46（美元）。可以看出0.5%的月风险溢价会使投资的总收益比无风险国债多3倍多，这就是复利的作用。你可能会问既然如此为什么还会有人投资于国债，很明显这是一个风险的超额收益问题。那么风险与收益这种权衡关系的本质是什么呢？一个长期收益率波动的投资风险较难理解，因此对它的刻画十分重要。

仿照之前的例子，我们继续用二叉树来构造一个股票基金终值的概率分布。与之前不同的是，这次不采用月利润简单相加，而是根据分布确定一个收益率并以之按复利计算终值。例如，假设某个股票组合的月收益率可以近似看成如下分布：月收益率50%的可能性是5.54%，50%的可能性是-3.54%。这种构造的月期望收益是1%，其风险用月收益标准差来衡量是  。2个月后的事件树如下所示：

300个月后二叉树会产生301种不同的可能结果，而每种结果的概率可以通过Excel中的BINOMDIST函数来获得。由此我们计算得到期末终值的均值为19.79，标准差为18.09。我们可以用这个标准差来度量19.79-4.29=15.5（1550%）的风险溢价吗？回想之前小节里讲的收益分布的非对称性会使标准差衡量的风险水平出现偏差的情况，所以我们必须先看看这个事件树最终的分布情况。

图5-9画出了期末可能价值的发生概率，可以看出分布的非对称性是很明显的。很高的正偏度表明标准差对风险的度量并不适用。实际上，以复利计算多期二项分布的终值时，其收敛于 对数正态分布 （lognormal distribution） 。对数正态分布描述的变量在取对数后服从正态分布。

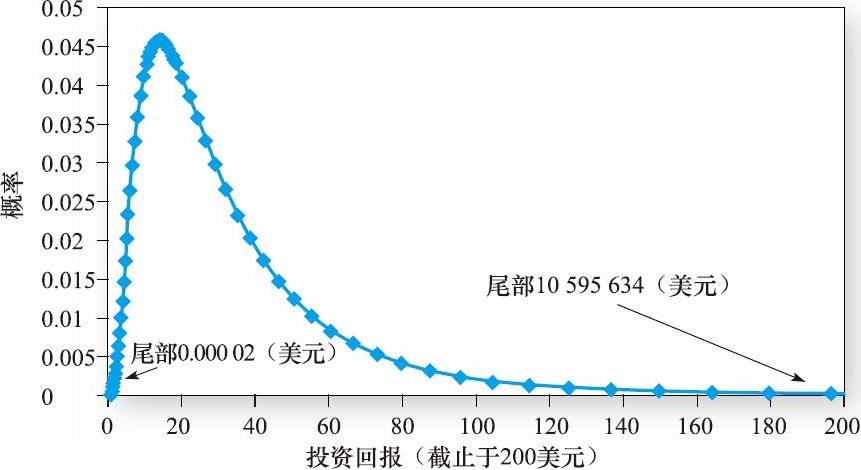
图5-9 25年后的概率分布服从对数正态分布

关注【叩富问财】服务号，关注后在对话框回复“长期投资”，可获得关于长期投资的最新热点、必学知识、视频讲解、一对一顾问讲解等服务。点击微信，一键关注