风险厌恶和效用价值
发布时间:2021-1-14 14:49阅读:4211
风险厌恶和效用价值
第5章中展示了不同类型资产的收益率以及大量深入的实证研究,表明风险资产都需要风险溢价作为补偿,这说明大多数投资者都是风险厌恶的。
风险厌恶(risk averse) 的投资者会放弃公平赌局和更差的投资。他们更愿意考虑无风险资产和有正风险溢价的投资品。广泛地说,风险厌恶的投资者会“处罚”除去风险组合一定的收益率,以弥补其承担的风险。风险越大,处罚就越大。有人会疑问为什么一定要假设投资者是风险厌恶的,相信多数投资者都会同意这一观点,我们会在本章附录中进行详尽的讨论。
表6-1 可供选择的风险资产组合(无风险利率为5%)
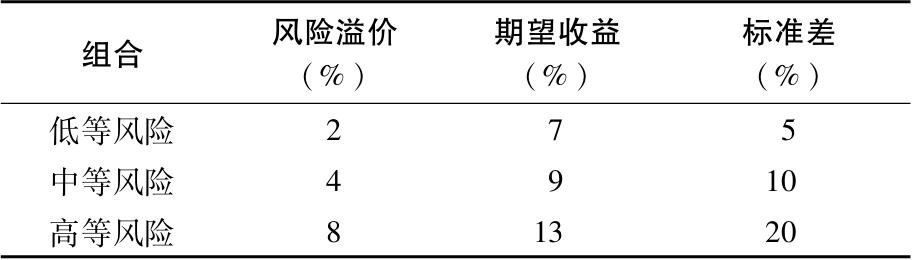
为了阐述在众多风险水平不同的投资组合中进行选择将会面临的问题,我们给出一个具体的例子。假设无风险利率是5%,投资者面临表6-1中3种不同的投资组合。表中用风险溢价、风险水平和标准差(SD)来说明低风险债券(L)、高风险债券(M)和股票组合(H)的风险收益特征。投资者会如何选择呢?
我们假设投资者会根据收益风险情况为每个资产组合给出一个效用值分数。分数越高说明这个资产组合越有吸引力。资产期望收益越高分数越高,波动性越大分数越低。业界存在很多的打分方法。金融学和特许金融分析师机构应用最多的一个效用函数是

U是效用值,A是投资者的风险厌恶系数。系数1/2只是一个约定俗成的数值。使用式(6-1)时,收益率必须采用小数形式而不是百分数。
式(6-1)同样表明了效用随期望收益的增加和风险的减少而增加。注意,无风险资产的效用值就是其自身的收益率,因为其风险补偿为零。风险资产方差降低,资产效用值的程度由风险厌恶系数A决定。投资者对风险厌恶程度越高(A越大),对风险要求的补偿就越高。投资者会在投资产品中选择其效用值最高的组合,后面的专栏6-1会讨论财务顾问度量其客户的投资风险厌恶程度的一些方法。
【例6-1】通过效用得分评估投资考虑3个风险厌恶程度不同的投资者:A 1 =2,A 2 =3.5,A 3 =5。他们3人都在评价表6-1中的3个投资组合。因为无风险利率为5%,用式(6-1)得到3个投资者对无风险资产的效用分数都是0.05。表6-2展示了他们对每个风险资产的打分情况。每个投资者最优的选择是用粗体显示的部分。
表6-2 几种投资组合对不同风险厌恶水平投资者的效用值

可以把风险资产的效用值看作投资者的 确定等价收益率 (certainty equivalent rate) ,即无风险资产未达到与风险资产相同的效用所需要的收益率。这个比率是比较不同组合带来效用值最自然最直接的方法。
现在可以说,只有当一个投资组合的确定等价收益率超过无风险收益率时,这个投资才是值得的。对于一个极度厌恶风险的投资者,任何风险组合甚至风险溢价为正的投资,其效用都有可能低于无风险资产,使得投资者拒绝风险资产组合。同时,风险厌恶程度较低的投资者可能从同样的风险资产组合中获得的效用高于无风险资产,从而愿意投资。如果风险溢价为零或负数,任何降低效用的调整都会使投资组合看起来更糟糕,所有风险厌恶投资者都会选择无风险资产。
和风险厌恶者相对的, 风险中性 (risk neutral) 投资者(其A=0)只根据风险资产的期望收益率来判断收益预期。风险的高低对风险中性投资者无关紧要,这意味着他们对风险要求的补偿为零。他们的确定等价收益率就是资产的期望收益率。
概念检查6-2一个资产组合期望收益率为20%,标准差30%,同时短期国债提供的无风险收益率为7%,一个风险厌恶系数A=4的投资者会在二者中如何选择?A=2呢?
风险偏好者 (risk lover) (其A<0)更加愿意参加公平博弈或其他赌博,这种投资者将风险的乐趣考虑在内后上调了效用水平。风险偏好者总是愿意参加公平博弈,因为公平博弈的确定等价收益率高于无风险收益率。
通过对投资者认为效用相同的投资组合风险收益描点,我们可以得到投资者风险与收益的权衡。横轴是期望收益,纵轴是标准差。图6-1画出了资产组合P的情况。
资产组合P(期望收益为E(r P ),标准差为σ P ),与第Ⅳ象限的所有组合相比期望收益更高,标准差更小,所以更受风险厌恶者的青睐。相反,第Ⅰ象限的所有组合都比P组合受欢迎,因为它们的期望收益大于等于E(r P ),标准差小于等于δ P 。
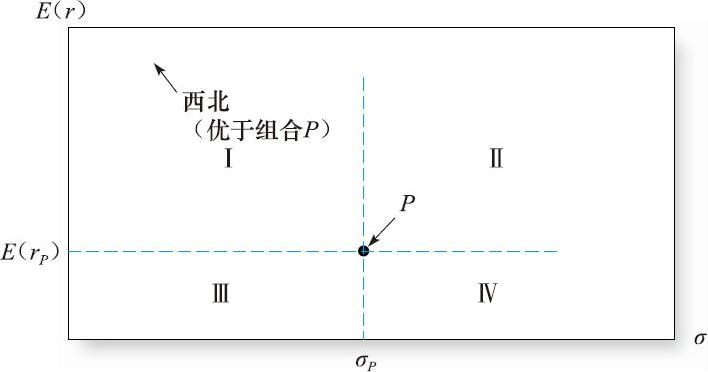
图6-1 某投资组合P的风险-收益权衡
这就是均值-标准差准则,或称 均值-方差准则 (mean-variance criterion,M-V) 。这可以表示为:投资组合A优于投资组合B,如果E(r A )≥E(r B )与σ A ≤σ B 至少有一个条件严格成立。
在图6-1中的期望收益标准差曲线,最受欢迎的方向是左上方向,因为这个方向提高了期望收益同时降低了方差。这意味着所有P点西北方向的任何组合都优于组合P。
那么第Ⅱ象限和第Ⅲ象限的投资组合又如何呢?与组合P相比,这些组合的受青睐程度完全取决于投资者的风险厌恶程度。假设投资者确认了所有和P一样好的投资组合,从P点开始,效用随标准差的增加而减少,这必须以期望收益率的提高作为补偿。因此对于投资者而言,图6-2中的Q点和P具有相同的吸引力。高风险高期望收益的资产和低风险低收益的组合对投资者的吸引力相同。在均值-标准差图表中,用一条曲线将这些效用相同的所有资产组合连在一起,就构成了 无差异曲线 (indifference curve) ,如图6-2所示。
为了检验无差异曲线上的点,我们用表6-3中A=4的投资者对曲线上不同投资组合的效用值进行计算。最终得到各资产组合的效用值相同,因为更高风险的资产组合有更高的期望收益。
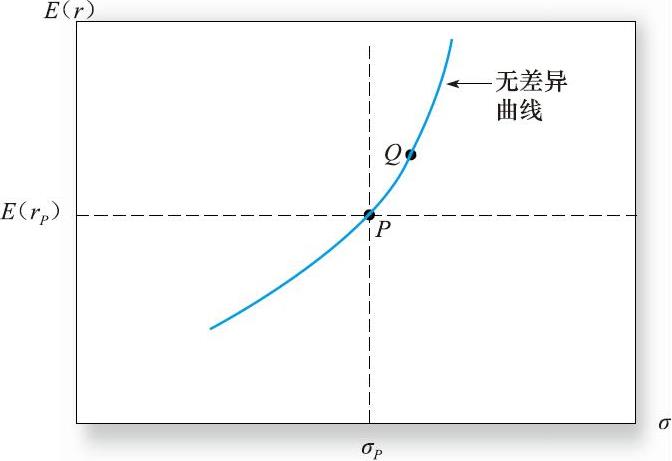
图6-2 无差异曲线
表6-3 风险厌恶系数A=4的投资者对示例投资组合的效用值
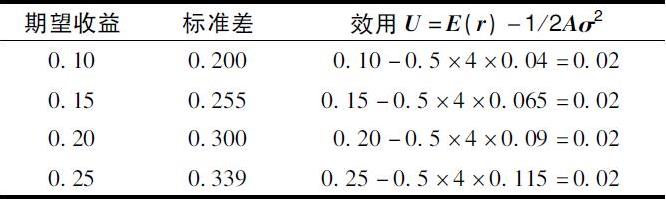
a.与图6-2的无差异曲线相比,一个风险厌恶程度更低的投资者的无差异曲线会如何变化?
b.画出过P点的两条无差异曲线。
温馨提示:投资有风险,选择需谨慎。


 问一问
问一问
 +微信
+微信
 分享该文章
分享该文章












